How Do The Number Of Nodal Planes Change As The L Quantum Number Of The Subshell Changes?

Chapter 2.5: Atomic Orbitals and Their Energies

1. Terminal updated

2. Salve every bit PDF

Folio ID

17397

Learning Objectives

• To apply the results of quantum mechanics to chemistry.

The paradox described by Heisenberg's doubtfulness principle and the wavelike nature of subatomic particles such every bit the electron made information technology incommunicable to use the equations of classical physics to describe the motion of electrons in atoms. Scientists needed a new approach that took the wave behavior of the electron into business relationship. In 1926, an Austrian physicist, Erwin Schrödinger (1887–1961; Nobel Prize in Physics, 1933), developed wave mechanics, a mathematical technique that describes the relationship betwixt the motion of a particle that exhibits wavelike properties (such as an electron) and its allowed energies. In doing so, Schrödinger's theory today is described as quantum mechanicsA theory developed past Erwin Schrödinger that describes the energies and spatial distributions of electrons in atoms and molecules. . It successfully describes the energies and spatial distributions of electrons in atoms and molecules.

Erwin Schrödinger (1887–1961)

Schrödinger's unconventional approach to atomic theory was typical of his unconventional approach to life. He was notorious for his intense dislike of memorizing data and learning from books. When Hitler came to power in Germany, Schrödinger escaped to Italia. He and then worked at Princeton University in the United States just eventually moved to the Institute for Avant-garde Studies in Dublin, Ireland, where he remained until his retirement in 1955.

Although quantum mechanics uses sophisticated mathematics, you do not need to empathize the mathematical details to follow our discussion of its general conclusions. We focus on the properties of the wave functions that are the solutions of Schrödinger's equations. The Schrödinger equation is similar in form to equations for the propagation of waves, which is why originally quantum mechanics was called moving ridge mechanics, just there are significant differences between quantum wave functions and those that describe real waves. Therefore, at this point it would exist best to lean only lightly on the standing wave analogy.

Wave Functions

A wavefunction (Ψ)A mathematical function that relates the location of an electron at a given signal in space to the aamplitude of its wave, which corresponds to its energy. , Ψ is the uppercase Greek alphabetic character psi, is a mathematical expression that can be used to calculate whatever property of an cantlet. In general, wavefunctions depend on both time and position. For atoms, solutions to the Schrödinger equation correspond to arrangements of the electrons, which, if left lone, remain unchanged and are thus only functions of position. To indicate time independence we use lower instance ψ

Wavefunctions for each atom have some properties that are exact, for instance each wavefunction describes an electron in quantum country with a specific energy. Each of these exact properties is associated with an integer. The energy of an electron in an atom is associated with the integer n, which turns out to be the same n that Bohr found in his model. These integers are called quantum numbers and dissimilar wavefunctions have different sets of quantum numbers. The of import indicate nearly breakthrough numbers is that they are countable integers, not continuous variables like the number of points on a line. In the instance of atoms, each electron has four quatum numbers which decide its wavefunction.

For other properties, there is a mathematical procedure by which the wavefunctions can exist used to summate boilerplate values and probabilities for anything, for instance the probability of finding the electron at any point in space. Driven by the Heisenberg Uncertainy Principle, the calculation of probabilities is the best we can do for properties not associated directly with quantum numbers.

The properties of wave functions derived from breakthrough mechanics are summarized hither. Although there are no equations in that location are a number of advanced concepts. Even if your math is not strong, try to understand the cardinal concepts.:

• A fourth dimension contained wavefunction uses 3 variables to describe the position of an electron. Three coordinates specify the position in space (as with the Cartesian coordinates ten, y, and z, or spherical coordinates r, θ, φ). Figure 2.21 shows both Cartesian and spherical coordinates. For the motility of an electron nigh the massive nucleus, spherical coordinates tin can be more natural than Cartesian.

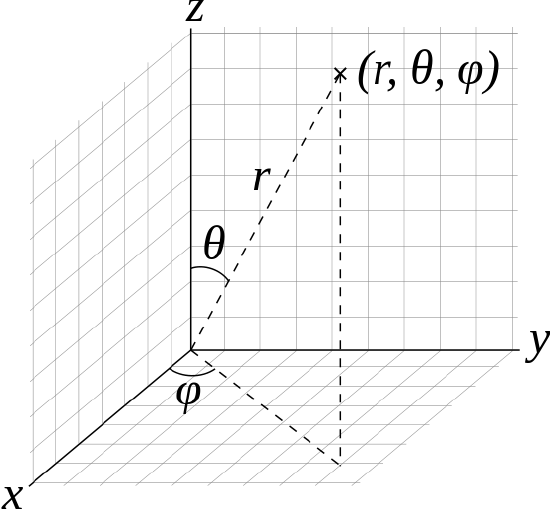
Figure two.5.1 Cartesian (10, y, z) and spherical coordinates (r, θ, φ)

• Wave functions have both real and imaginary parts. They are circuitous functions, which is a mathematical term indicating that they contain \( \sqrt{-ane} \)., represented every bit i. Imaginary and complex numbers take no physical significance.

Imaginary Numbers

If you lot demand an introduction to imaginary number, here is one. To see it y'all will have to be attached to the Internet

• The probability of finding an electron at a signal is given past the product of the moving ridge function ψ and its circuitous conjugate ψ * in which all terms that incorporate i are replaced by −i. This product is called the modulus square and for wave functions information technology always must be a existent positive number or nada. Negative, impaginary or complex probabilities of finding an electron at a point would be meaningless. This interpretation was discovered by Max Born, for which he won the Nobel prize. We utilize probabilities because, according to Heisenberg's doubt principle, we cannot precisely specify the position of an electron.

The probability of finding an electron at whatever point in space depends on several factors, including the quantum numbers specifying the wavefunction and the 3 coordinates specifying the position in space we are interested in. Equally one way of graphically representing the probability distribution, the probability of finding an electron is indicated past the density of colored dots, shown for the footing land of the hydrogen atom in Figure 2.5.2

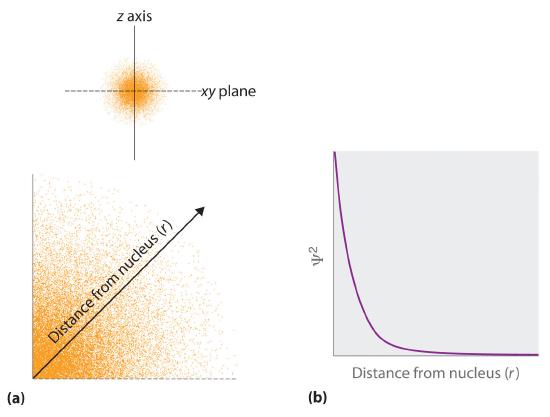
Figure 2.v.2 Probability of Finding the Electron in the Basis State of the Hydrogen Atom at Different Points in Space (a) The density of the dots shows electron probability. (b) In this plot of Ψ² versus r for the footing state of the hydrogen cantlet, the electron probability density is greatest at r = 0 (the nucleus) and falls off with increasing r. Because the line never really reaches the horizontal axis, the probability of finding the electron at very big values of r is very modest only not zero.

• The total probability of finding the electron anywhere must be 100%. It has to exist somewhere. On the other paw, since there is a lot more infinite far away from a nucleus than near it, the probability of finding the electron at whatever one point every bit one moves away from the nucleus must eventually go to zero.
• The relative phases of wave role for electrons in different atoms determines bonding. This will be of import in our discussion of chemical bonding in Chapter v. Every bit discussed in the previous section, wavefunctions like waves, tin positively reinforce each other or destructively interfere. When they reinforce they are said to be in phase, and when they interfere they are said to be out of stage. The phases are indicated as positive, +, or negative, -. Do not confuse the sign of the phase with a positive or negative electrical charge.
• Each wavefunction has a unique sets of quantum numbersA unique set of numbers that specifies a wave function (a solution to the Schrödinger equation), which provides of import information about the free energy and spatial distribution of an electron. . The spacial patterns of the three-dimensional wave functions are complex. Fortunately, still, in the 18th century, a French mathematician, Adrien Legendre (1752–1783), developed a fix of equations to describe the movement of tidal waves on the surface of a h2o world, which turn out to exist solutions of the Schrödinger equation for a spherically symmetric cantlet.
• Each wave function is associated with a particular energy. As in Bohr's model, the energy of an electron in an cantlet is quantized; information technology can have only certain immune values. The major difference betwixt Bohr'south model and Schrödinger's arroyo is that Bohr had to impose the idea of quantization arbitrarily, whereas in Schrödinger's approach, quantization emerges from the moving ridge equation.

Quantum Numbers

Schrödinger's arroyo requires three quantum numbers (n, 50, and m _l ) to specify a wave function for each electron. The quantum numbers provide information about the spatial distribution of an electron. Although north can be whatever positive integer (NOT zip), but sure values of l and grand _fifty are allowed for a given value of n. This is a result of the mathematical details of the Schrödinger equation

The Chief Quantum Number

The master quantum number (n)I of three quantum numbers that tells the boilerplate relative distance of an electron from the nucleus. indicates the energy of the electron and the average distance of an electron from the nucleus:

Equation two.v.ane n = 1, 2, iii, 4,…

As n increases for a given atom, so does the average distance of an electron from the nucleus. A negatively charged electron that is, on boilerplate, closer to the positively charged nucleus is attracted to the nucleus more strongly than an electron that is farther out in space. This means that electrons with higher values of n are easier to remove from an cantlet. All moving ridge functions that have the same value of n are said to constitute a main shellAll the wave functions that have the aforementioned value of because those electrons accept similar average distances from the nucleus. because those electrons have like boilerplate distances from the nucleus. As you lot volition meet, the principal quantum number n corresponds to the n used past Bohr to depict electron orbits and by Rydberg to describe atomic free energy levels.

The Azimuthal Quantum Number

The second quantum number is often called the azimuthal quantum number (l)I of three quantum numbers that discribes the shape of the region of space occupied by an electron. . The value of l describes the shape of the region of infinite occupied by the electron. The allowed values of l depend on the value of n and tin can range from 0 to north − 1:

Equation 2.5.2 l = 0, one, two,…, n − 1

For example, if n = ane, l can be only 0; if n = two, l can be 0 or 1; and then forth. For a given atom, all wave functions that accept the aforementioned values of both north and 50 form a subshellA group of wave functions that have the same values of <math xml:id="av_1.0-ch02_m046" display="inline"><semantics><mi>northward</mi></semantics></math> and <math xml:id="av_1.0-ch02_m047" brandish="inline"><semantics><mrow><mi>l</mi><mo>.</mo></mrow></semantics></math> . The regions of infinite occupied past electrons in the aforementioned subshell usually have the same shape, but they are oriented differently in infinite.

The Magnetic Breakthrough Number

The tertiary quantum number is the magnetic quantum number (k _fifty )One of iii breakthrough numbers that describes the orientation of the region of space occupied by an electron with respect to an applied magnetic field. . The value of m _l describes the orientation of the region in space occupied by an electron with respect to an applied magnetic field. The immune values of one thousand _l depend on the value of l: one thousand _fifty tin range from −l to l in integral steps:

Equation ii.five.three m _fifty = − l , − l + 1,…, 0,…, fifty − 1, l

For example, if l = 0, yard _fifty tin be only 0; if l = 1, m _l tin be −one, 0, or +ane; and if fifty = 2, g _l tin be −ii, −1, 0, +ane, or +2.

Each wave function with an allowed combination of n, l, and chiliad _l values describes an atomic orbital A wave function with an allowed combination of due north, 50 and m_l quantum numbers. , a particular spatial distribution for an electron. For a given set of quantum numbers, each principal beat has a fixed number of subshells, and each subshell has a fixed number of orbitals.

Example 2.v.one

How many subshells and orbitals are contained within the principal beat out with due north = 4?

Given: value of due north

Asked for: number of subshells and orbitals in the primary crush

Strategy:

A Given n = iv, calculate the immune values of l. From these allowed values, count the number of subshells.

B For each allowed value of l, calculate the immune values of m _l . The sum of the number of orbitals in each subshell is the number of orbitals in the principal shell.

Solution:

A We know that l tin can have all integral values from 0 to n − one. If north = four, and then l can equal 0, i, 2, or 3. Because the shell has 4 values of l, information technology has 4 subshells, each of which will comprise a different number of orbitals, depending on the allowed values of m ₅₀ .

B For l = 0, chiliad _l can be only 0, and thus the 50 = 0 subshell has only one orbital. For l = 1, thou _l can exist 0 or ±1; thus the l = 1 subshell has iii orbitals. For 50 = 2, m _fifty tin be 0, ±1, or ±ii, and then there are five orbitals in the l = 2 subshell. The last immune value of l is l = 3, for which thousand _l can be 0, ±1, ±ii, or ±3, resulting in vii orbitals in the l = three subshell. The full number of orbitals in the n = 4 principal shell is the sum of the number of orbitals in each subshell and is equal to northward ²:

\( \mathop ane\limits_{(50 = 0)} + \mathop 3\limits_{(l = 1)} + \mathop 5\limits_{(l = 2)} + \mathop 7\limits_{(l = three)} = 16\; {\rm{orbitals}} = {(four\; {\rm{principal\: shells}})^2} \)​

Exercise

How many subshells and orbitals are in the principal beat with n = 3?

Answer: three subshells; nine orbitals

Rather than specifying all the values of n and 50 every fourth dimension we refer to a subshell or an orbital, chemists use an abbreviated organisation with lowercase letters to denote the value of fifty for a detail subshell or orbital:

l =	0	ane	2	3
Designation	due south	p	d	f

The principal quantum number is named start, followed by the letter south, p, d, or f every bit appropriate. These orbital designations are derived from corresponding spectroscopic characteristics of lines involving them: due southharp, principle, diffuse, and fundamental. A anes orbital has n = i and l = 0; a 2p subshell has n = 2 and fifty = 1 (and has three 2p orbitals, corresponding to m _l = −1, 0, and +1); a 3d subshell has n = 3 and l = 2 (and has five 3d orbitals, corresponding to m ₅₀ = −2, −ane, 0, +1, and +2); and so forth.

We tin can summarize the relationships between the breakthrough numbers and the number of subshells and orbitals equally follows (Table two.v.1 ):

• Each principal shell has n subshells. For n = one, just a single subshell is possible (1south); for n = two, at that place are 2 subshells (2due south and 2p); for n = 3, there are three subshells (3s, iiip, and 3d); and so forth. Every shell has an ns subshell, whatever shell with n ≥ ii besides has an np subshell, and any shell with n ≥ iii also has an nd subshell. Because a iid subshell would require both n = ii and l = 2, which is not an allowed value of l for n = two, a twod subshell does non be.
• Each subshell has 2l + 1 orbitals. This means that all ns subshells contain a single southward orbital, all np subshells contain three p orbitals, all nd subshells contain v d orbitals, and all nf subshells comprise seven f orbitals.

Note the Pattern

Each principal shell has northward subshells, and each subshell has 2l + one orbitals.

Table 2.five.1 Immune v alues of n, l, and m₅₀ through north = 4

n	l	Subshell Designation	m fifty	Number of Orbitals in Subshell	Number of Orbitals in Beat
1	0	1s	0	one	1
2	0	2due south	0	i	4
	1	2p	−one, 0, 1	iii
3	0	3s	0	1	9
	1	threep	−one, 0, 1	3
	2	3d	−2, −1, 0, 1, 2	five
4	0	4s	0	1	16
	1	fourp	−ane, 0, 1	3
	two	fourd	−ii, −1, 0, ane, 2	5
	3	4f	−three, −2, −one, 0, ane, 2, 3	7

Orbital Shapes

An orbital is the quantum mechanical generalization of Bohr'southward orbit. In contrast to his concept of a simple circular orbit with a stock-still radius, orbitals are mathematically derived regions of infinite with different probabilities of having an electron.

One style of representing electron probability distributions was illustrated in Figure two.v.1 for the 1due south orbital of hydrogen. The probability of finding an electron in a region of infinite with volume V (such as a cubic picometer) is the product of the volume with ψ ψ ^*(nosotros tin write this as |ψ| ²). From our consideration of the properties of the wavefunction, we know that adding up the probability from every such small volume over all space will sum to unity, or a 100% probability that the electron is somewhere. A plot of |ψ| ² versus distance from the nucleus (r) is a plot of the probability density. The 1s orbital is spherically symmetrical, so the probability of finding a is electron at any given betoken depends only on its distance from the nucleus. The probability density is greatest at r = 0 (at the nucleus) and decreases steadily with increasing distance. At very big values of r, the electron probability density is tiny merely not eactly zippo.

In dissimilarity to the probability density, nosotros can calculate the radial probability (the probability of finding a 1s electron at a distance r from the nucleus) by adding together the probabilities of an electron being at all points on a series of x spherical shells of radius r _ane, r ₂, r ₃,…, r _{x − one}, r ₁₀ . In outcome, we are dividing the atom into very thin concentric shells, much like the layers of an onion (function (a) in Figure 2.5.2 ), and calculating the probability of finding an electron on each spherical trounce. Call up that the electron probability density is greatest at r = 0 (part (b) in Effigy ii.5.three ), then the density of dots is greatest for the smallest spherical shells in part (a) in Effigy two.v.3

By contrast, the surface area of each spherical shell is equal to 4πr ⁱⁱ, which increases rapidly with increasing r (role (c) in Figure 2.5.iii ). Considering the surface surface area of the spherical shells increases at starting time more rapidly with increasing r than the electron probability density decreases, the plot of radial probability has a maximum at a item distance (part (d) in Figure 2.5.3 ). As of import, when r is very small, the surface area of a spherical shell is and then small that the total probability of finding an electron close to the nucleus is very low; at the nucleus, the electron probability vanishes because the surface area of the beat out is nada (part (d) in Figure 2.v.2 ).

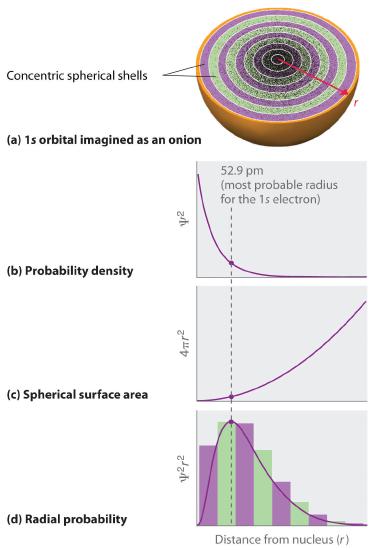
Figure 2.5.3 Nearly Likely Radius for the Electron in the Ground State of the Hydrogen Cantlet (a) Imagine dividing the atom's total volume into very thin concentric shells equally shown in the onion drawing. (b) A plot of electron probability density Ψ² versus r shows that the electron probability density is greatest at r = 0 and falls off smoothly with increasing r. The density of the dots is therefore greatest in the innermost shells of the onion. (c) The surface area of each crush, given by 4πr ², increases rapidly with increasing r. (d) If we count the number of dots in each spherical crush, nosotros obtain the total probability of finding the electron at a given value of r. Because the surface surface area of each shell increases more than rapidly with increasing r than the electron probability density decreases, a plot of electron probability versus r (the radial probability) shows a peak. This peak corresponds to the about probable radius for the electron, 52.9 pm, which is exactly the radius predicted by Bohr'south model of the hydrogen atom.

For the hydrogen atom, the meridian in the radial probability plot occurs at r = 0.529 Å (52.nine pm), which is exactly the radius calculated by Bohr for the n = one orbit. Thus the nigh probable radius obtained from quantum mechanics is identical to the radius calculated by classical mechanics. In Bohr'south model, however, the electron was assumed to be at this distance 100% of the fourth dimension, whereas in the Schrödinger model, information technology is at this distance simply some of the time. The difference betwixt the two models is attributable to the wavelike behavior of the electron and the Heisenberg Uncertainty Principle.

Figure 2.5,iv compares the electron probability densities for the hydrogen 1s, twos, and iiis orbitals. Note that all three are spherically symmetrical. For the 2s and threes orbitals, even so (and for all other s orbitals as well), the electron probability density does not autumn off smoothly with increasing r. Instead, a series of minima and maxima are observed in the radial probability plots (function (c) in Figure 2.five.iv ). The minima correspond to spherical nodes (regions of zero electron probability), which alternating with spherical regions of nonzero electron probability.

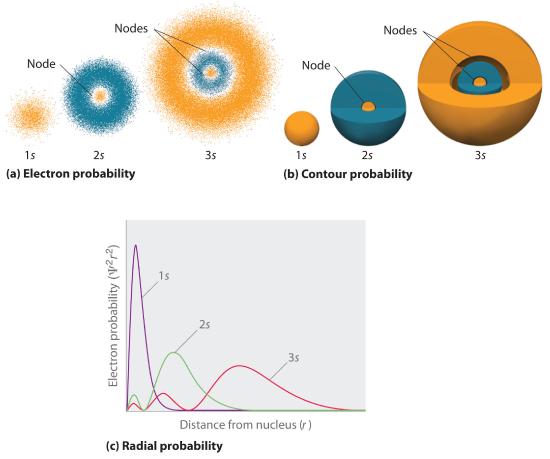
Figure 2.5.4 Probability Densities for the 1s, 2s, and iiidue south Orbitals of the Hydrogen Cantlet (a) The electron probability density in any plane that contains the nucleus is shown. Notation the presence of circular regions, or nodes, where the probability density is zero. (b) Contour surfaces enclose 90% of the electron probability, which illustrates the unlike sizes of the onesouth, iis, and 3due south orbitals. The cutaway drawings give partial views of the internal spherical nodes. The orange color corresponds to regions of space where the phase of the wave function is positive, and the blueish color corresponds to regions of infinite where the phase of the wave function is negative. (c) In these plots of electron probability as a office of distance from the nucleus (r) in all directions (radial probability), the most probable radius increases equally n increases, but the 2due south and 3s orbitals have regions of significant electron probability at modest values of r.

due south Orbitals

Three things happen to s orbitals as northward increases (Effigy 2.5.4 ):

1. They become larger, extending farther from the nucleus.
2. They contain more nodes. This is similar to a standing wave that has regions of significant amplitude separated by nodes, points with zip amplitude.
3. For a given atom, the due south orbitals also become college in free energy as n increases because of their increased distance from the nucleus.

Orbitals are mostly drawn as three-dimensional surfaces that enclose 90% of the electron densityElectron distributions that are represented as standing waves. , every bit was shown for the hydrogen 1s, 2s, and threes orbitals in part (b) in Effigy two.5.iv Although such drawings bear witness the relative sizes of the orbitals, they practice not unremarkably show the spherical nodes in the 2due south and 3due south orbitals because the spherical nodes lie inside the xc% surface. Fortunately, the positions of the spherical nodes are non important for chemical bonding. This makes sense because bonding is an interaction of electrons from two atoms which will be most sensitive to forces at the edges of the orbitals.

p Orbitals

Only s orbitals are spherically symmetrical. As the value of l increases, the number of orbitals in a given subshell increases, and the shapes of the orbitals get more circuitous. Because the 2p subshell has l = 1, with three values of k _fifty (−i, 0, and +i), in that location are three 2p orbitals.

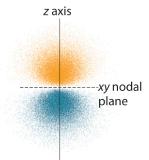
Effigy 2.5.v Electron Probability Distribution for a Hydrogen 2p Orbital The nodal plane of zip electron density separates the two lobes of the twop orbital. Every bit in Effigy 2.5.4 , the colors correspond to regions of space where the phase of the wave role is positive (orange) and negative (blue).

The electron probability distribution for 1 of the hydrogen iip orbitals is shown in Figure 2.5.5 . Considering this orbital has two lobes of electron density arranged forth the z axis, with an electron density of zero in the xy plane (i.due east., the xy plane is a nodal plane), it is a 2p _z orbital. As shown in Figure ii.5.six , the other two 2p orbitals accept identical shapes, but they prevarication along the ten centrality (2p _x ) and y axis (2p _y ), respectively. Note that each p orbital has just one nodal plane. In each case, the stage of the wave function for each of the twop orbitals is positive for the lobe that points forth the positive axis and negative for the lobe that points forth the negative axis. Information technology is important to emphasize that these signs correspond to the phase of the wave that describes the electron motion, not to positive or negative charges.

In the side by side section when nosotros consider the electron configuration of multielectron atoms, the geometric shapes provide an important clue near which orbitals volition be occupied by dissimilar electrons. Considering electrons in unlike p orbitals are geometrically distant from each other, there is less repulsion between them than would be found if 2 electrons were in the same p orbital. Thus, when the p orbitals are filled, information technology volition be energetically favorable to place i electron into each p orbital, rather than two into one orbital.

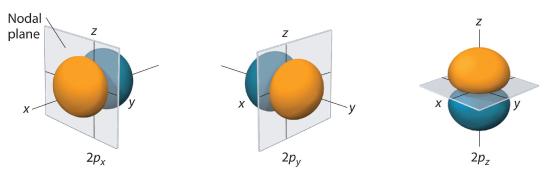
Figure two.v.6 The Iii Equivalent 2p Orbitals of the Hydrogen Atom The surfaces shown enclose 90% of the total electron probability for the twop _x , twop _y , and 2p _z orbitals. Each orbital is oriented along the axis indicated by the subscript and a nodal plane that is perpendicular to that axis bisects each iip orbital. The stage of the wave function is positive (orange) in the region of infinite where 10, y, or z is positive and negative (bluish) where x, y, or z is negative.

Simply as with the s orbitals, the size and complexity of the p orbitals for any atom increase as the chief quantum number n increases. The shapes of the 90% probability surfaces of the 3p, 4p, and college-energy p orbitals are, however, essentially the same every bit those shown in Figure 2.five.vi

d Orbitals

Subshells with 50 = 2 take 5 d orbitals; the first principal trounce to have a d subshell corresponds to n = iii. The five d orbitals accept yard _l values of −2, −1, 0, +1, and +2.

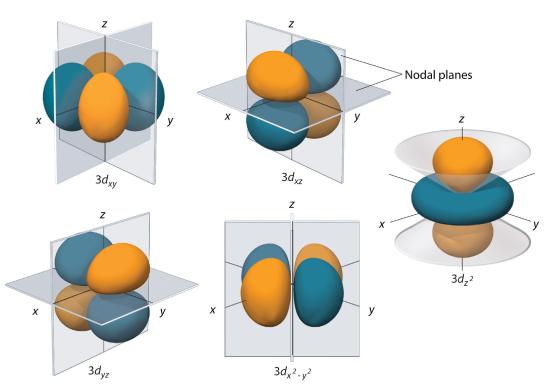
Effigy 2.5.7 The Five Equivalent threed Orbitals of the Hydrogen Atom The surfaces shown enclose 90% of the total electron probability for the five hydrogen threed orbitals. Four of the five 3d orbitals consist of iv lobes arranged in a plane that is intersected by ii perpendicular nodal planes. These four orbitals have the aforementioned shape just dissimilar orientations. The 5th 3d orbital, \( 3d_{z^{2}}​ \) ​, has a distinct shape even though information technology is mathematically equivalent to the others. The phase of the wave function for the unlike lobes is indicated past color: orange for positive and blue for negative.

The hydrogen 3d orbitals, shown in Effigy 2.5.vii , have more complex shapes than the 2p orbitals. All 5 threed orbitals incorporate two nodal surfaces, equally compared to i for each p orbital and cypher for each south orbital. In three of the d orbitals, the lobes of electron density are oriented betwixt the x and y, x and z, and y and z planes; these orbitals are referred to as the 3d _xy , iiid _xz , and threed _yz orbitals, respectively. A 4th d orbital has lobes lying along the x and y axes; this is the \( 3d_{x^{two}-y^{2}} \) orbital. The fifth iiid orbital, chosen the \( 3d_{z^{ii}}​ \) orbital, has a unique shape: it looks like a twop _z orbital combined with an boosted doughnut of electron probability lying in the xy plane. Despite its peculiar shape, the \( 3d_{z^{ii}}​ \)​ orbital is mathematically equivalent to the other 4 and has the same energy. In contrast to p orbitals, the phase of the moving ridge function for d orbitals is the same for contrary pairs of lobes. As shown in Figure 2.5.7 , the phase of the moving ridge role is positive for the two lobes of the \( 3d_{z^{two}}​ \)​ orbital that lie along the z centrality, whereas the phase of the moving ridge function is negative for the doughnut of electron density in the xy airplane. Like the south and p orbitals, as due north increases, the size of the d orbitals increases, but the overall shapes remain similar to those depicted in Effigy 2.5.7 .

f Orbitals

Principal shells with n = 4 tin can have subshells with 50 = 3 and m ₅₀ values of −3, −2, −i, 0, +1, +2, and +iii. These subshells consist of seven f orbitals. Each f orbital has iii nodal surfaces, so their shapes are complex. Considering f orbitals are not peculiarly important for our purposes, we practise not talk over them further, and orbitals with college values of 50 are non discussed at all. Equivalent illustrations of the shapes of the f orbitals are bachelor

Orbital Energies

Although we have discussed the shapes of orbitals, we have said little about their comparative energies. We brainstorm our word of orbital energiesA item energy associated with a given set of quantum numbers. by because atoms or ions with only a single electron (such every bit H or He⁺). This is the simplest case.

The relative energies of the atomic orbitals with north ≤ four for a hydrogen atom are plotted in Effigy 2.5.viii notation that the orbital energies depend on only the principal quantum number n. Consequently, the energies of the 2south and 2p orbitals of hydrogen are the same; the energies of the 3s, 3p, and 3d orbitals are the aforementioned; and so along. The orbital energies obtained for hydrogen using breakthrough mechanics are exactly the same every bit the allowed energies calculated by Bohr. In contrast to Bohr'due south model, however, which allowed only one orbit for each energy level, quantum mechanics predicts that there are 4 orbitals with different electron density distributions in the north = ii primary crush (i 2s and three 2p orbitals), nine in the n = 3 primary shell, and sixteen in the n = 4 master crush.The different values of l and m _l for the individual orbitals within a given principal shell are not important for understanding the emission or assimilation spectra of the hydrogen cantlet under most conditions, merely they do explain the splittings of the main lines that are observed when hydrogen atoms are placed in a magnetic field. As we have simply seen, however, quantum mechanics also predicts that in the hydrogen atom, all orbitals with the same value of n (e.chiliad., the iii 2p orbitals) are degenerateHaving the same energy. , meaning that they have the aforementioned energy. Figure two.5.8 shows that the energy levels go closer and closer together as the value of n increases, as expected because of the 1/due north ² dependence of orbital energies.

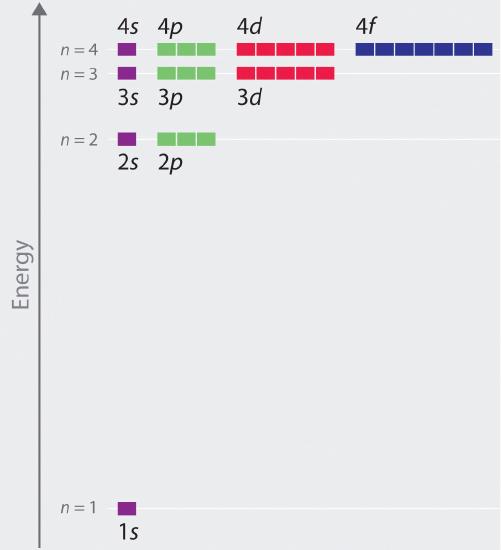
Figure 2.v.8 Orbital Energy Level Diagram for the Hydrogen Atom Each box corresponds to 1 orbital. Note that the difference in energy between orbitals decreases rapidly with increasing values of north.

The energies of the orbitals in whatever species with only one electron can exist calculated past a small-scale variation of Bohr's equation (Equation 2.iii.3), which can be extended to other single-electron species by incorporating the nuclear charge Z (the number of protons in the nucleus):

Equation 2.5.four \( E=-\frac{Z^{2}}{n^{2}}\mathcal{R}hc \)

In general, both energy and radius decrease every bit the nuclear charge increases. As a result of the Z^two dependence of free energy in Equation 2.24, electrons in the 1s orbital of carbon, which has a nuclear accuse of +6, prevarication roughly 36 times lower in energy than those in the hydrogen 1s orbital, and the 1s orbital of tin, with an diminutive number of 50 is roughly 2500 times lower still. The most stable and tightly bound electrons are in orbitals (those with the lowest energy) closest to the nucleus.

For example, in the ground state of the hydrogen atom, the single electron is in the anes orbital, whereas in the first excited state, the atom has captivated energy and the electron has been promoted to one of the n = 2 orbitals. In ions with only a single electron, the energy of a given orbital depends on only north, and all subshells within a principal crush, such every bit the p _x , p _y , and p _z orbitals, are degenerate.

Effective Nuclear Charges

For an cantlet or an ion with just a unmarried electron, we can summate the potential energy past considering but the electrostatic allure between the positively charged nucleus and the negatively charged electron. When more than i electron is present, yet, the full energy of the atom or the ion depends not but on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. When there are two electrons, the repulsive interactions depend on the positions of both electrons at a given instant, but because nosotros cannot specify the exact positions of the electrons, information technology is impossible to exactly summate the repulsive interactions. Consequently, we must use approximate methods to deal with the consequence of electron-electron repulsions on orbital energies.

If an electron is far from the nucleus (i.eastward., if the distance r between the nucleus and the electron is large), then at any given moment, virtually of the other electrons will exist betwixt that electron and the nucleus. Hence the electrons volition abolish a portion of the positive charge of the nucleus and thereby decrease the bonny interaction between it and the electron farther away. Equally a result, the electron farther away experiences an constructive nuclear charge (Z _eff)The nuclear accuse an electron actually experiences because of shielding from other electrons closer to the nucleus. that is less than the bodily nuclear charge Z. This issue is called electron shieldingThe effect by which electrons closer to the nucleus neutralize a portion of the positive accuse of the nucleus and thereby decrease the bonny interaction between the nucleus and an electron begetter away. . As the altitude between an electron and the nucleus approaches infinity, Z _eff approaches a value of 1 because all the other (Z − 1) electrons in the neutral atom are, on the average, between it and the nucleus. If, on the other hand, an electron is very close to the nucleus, then at any given moment about of the other electrons are further from the nucleus and do not shield the nuclear accuse. At r ≈ 0, the positive charge experienced by an electron is approximately the total nuclear charge, or Z _eff ≈ Z. At intermediate values of r, the effective nuclear accuse is somewhere betwixt 1 and Z: i ≤ Z _eff ≤ Z. Thus the actual Z _eff experienced past an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital only also on the distribution of all the other electrons present. This leads to large differences in Z _eff for different elements, as shown in Figure 2.v.ix for the elements of the kickoff 3 rows of the periodic table. Notice that only for hydrogen does Z _eff = Z, and merely for helium are Z _eff and Z comparable in magnitude.

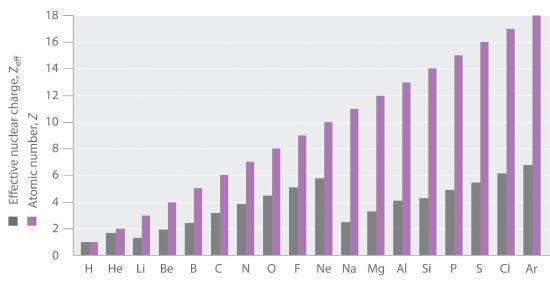
Figure 2.5.ix Relationship between the Effective Nuclear Accuse Z _eff and the Atomic Number Z for the Outer Electrons of the Elements of the First 3 Rows of the Periodic Table Except for hydrogen, Z _eff is ever less than Z, and Z _eff increases from left to right as you lot go across a row.

The trend that you see in Figure 2.5.9 for the beginning three principal shells corresponding to due north= 1, ii, and three, continues in the further shells. The atomic number and thus the nuclear charge increase linearly, but the sawtooth pattern for Z _eff repeats itself, resetting every bit the quantum number n changes. Chemical bonding and reactivity involves the sharing or commutation of electrons betwixt atoms. Those electrons which tin can participate are those held least strongly by the cantlet, the outermost electrons, which, no affair what the atomic number, and nuclear accuse, are bound to their atom past roughly the same energy range because of the shielding effect.

In multielectron atoms this shifts the energies of the different orbitals for a typical multielectron cantlet as shown in Figure ii.5.x . Within a given principal beat of a multielectron atom, the orbital energies increment with increasing 50. An ns orbital always lies beneath the corresponding np orbital, which in plow lies beneath the nd orbital. These free energy differences are caused past the effects of shielding and penetration, the extent to which a given orbital lies inside other filled orbitals. As shown in Figure 2.v.xi for example, an electron in the 2s orbital penetrates inside a filled is orbital more than an electron in a iip orbital does. Hence in an atom with a filled anesouth orbital, the Z _eff experienced by a 2s electron is greater than the Z _eff experienced by a twop electron. Consequently, the 2s electron is more tightly bound to the nucleus and has a lower free energy, consistent with the society of energies shown in Figure 2.5.x

Annotation the Pattern

Due to electron shielding, Z_eff increases more rapidly going across a row of the periodic table than going down a cavalcade.

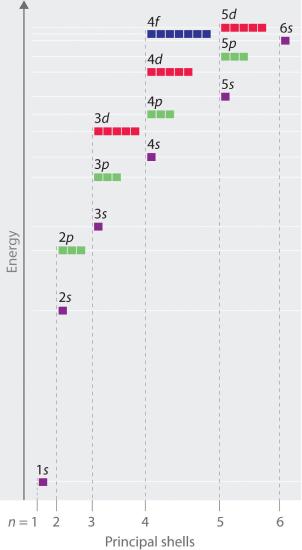
Figure ii.5.10 Orbital Energy Level Diagram for a Typical Multielectron Cantlet

Because of the effects of shielding and the different radial distributions of orbitals with the same value of n only different values of l, the different subshells are non degenerate in a multielectron atom. (Compare this with Figure 2.five.eight For a given value of due north, the ns orbital is always lower in energy than the np orbitals, which are lower in energy than the nd orbitals, and so forth. As a result, some subshells with higher principal quantum numbers are really lower in energy than subshells with a lower value of n; for example, the 4south orbital is lower in energy than the 3d orbitals for virtually atoms.

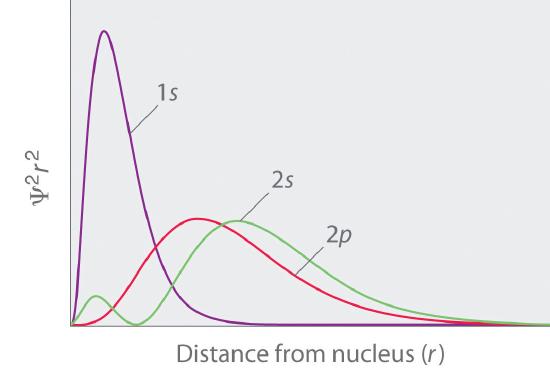
Figure 2.v.11 Orbital Penetration A comparing of the radial probability distribution of the 2s and twop orbitals for various states of the hydrogen cantlet shows that the 2south orbital penetrates inside the 1s orbital more than the 2p orbital does. Consequently, when an electron is in the modest inner lobe of the 2due south orbital, it experiences a relatively large value of Z _eff, which causes the energy of the 2due south orbital to be lower than the energy of the iip orbital.

Notice in Figure 2.five.ten that the difference in energies between subshells can be so big that the energies of orbitals from unlike chief shells can get approximately equal. For example, the free energy of the threed orbitals in most atoms is actually betwixt the energies of the 4s and the 4p orbitals.

Primal Equation

free energy of hydrogen-like orbitals

Equation ii.5.4: \( Due east=-\dfrac{Z^{2}}{n^{ii}}\mathcal{R}hc \)

Summary

Because of moving ridge–particle duality, scientists must bargain with the probability of an electron being at a item point in space. To do and so required the development of quantum mechanics, which uses wave functions (Ψ) to describe the mathematical relationship between the motion of electrons in atoms and molecules and their energies. Wave functions have five important backdrop: (1) the wave role uses iii variables (Cartesian axes 10, y, and z) to describe the position of an electron; (2) the magnitude of the wave role is proportional to the intensity of the wave; (iii) the probability of finding an electron at a given bespeak is proportional to the square of the wave role at that point, leading to a distribution of probabilities in space that is often portrayed as an electron density plot; (4) describing electron distributions as standing waves leads naturally to the existence of sets of breakthrough numbers characteristic of each moving ridge function; and (v) each spatial distribution of the electron described by a wave office with a given prepare of quantum numbers has a particular energy.

Quantum numbers provide important information about the energy and spatial distribution of an electron. The principal quantum number due north can be any positive integer; every bit north increases for an atom, the average altitude of the electron from the nucleus also increases. All moving ridge functions with the same value of n found a primary vanquish in which the electrons accept similar average distances from the nucleus. The azimuthal quantum number l can accept integral values between 0 and n − ane; it describes the shape of the electron distribution. Wave functions that have the aforementioned values of both n and fifty constitute a subshell, corresponding to electron distributions that usually differ in orientation rather than in shape or average altitude from the nucleus. The magnetic quantum number m _l can have 2l + ane integral values, ranging from −l to +50, and describes the orientation of the electron distribution. Each wave function with a given set of values of due north, l, and m _l describes a particular spatial distribution of an electron in an atom, an diminutive orbital.

The four chemically important types of atomic orbital represent to values of l = 0, one, ii, and 3. Orbitals with fifty = 0 are s orbitals and are spherically symmetrical, with the greatest probability of finding the electron occurring at the nucleus. All orbitals with values of n > 1 and fifty = 0 contain one or more nodes. Orbitals with l = i are p orbitals and contain a nodal plane that includes the nucleus, giving rise to a dumbbell shape. Orbitals with l = 2 are d orbitals and have more than complex shapes with at least two nodal surfaces. Orbitals with fifty = 3 are f orbitals, which are still more than complex.

Because its average distance from the nucleus determines the energy of an electron, each atomic orbital with a given set of quantum numbers has a particular energy associated with it, the orbital energy. In atoms or ions with simply a single electron, all orbitals with the same value of northward have the same energy (they are degenerate), and the energies of the primary shells increase smoothly as n increases. An atom or ion with the electron(southward) in the everyman-energy orbital(s) is said to be in its footing land, whereas an atom or ion in which one or more than electrons occupy higher-energy orbitals is said to be in an excited land.

The calculation of orbital energies in atoms or ions with more than ane electron (multielectron atoms or ions) is complicated by repulsive interactions between the electrons. The concept of electron shielding, in which intervening electrons human action to reduce the positive nuclear charge experienced by an electron, allows the apply of hydrogen-like orbitals and an effective nuclear charge (Z _eff) to describe electron distributions in more complex atoms or ions. The degree to which orbitals with different values of fifty and the same value of northward overlap or penetrate filled inner shells results in slightly different energies for dissimilar subshells in the same principal crush in almost atoms.

Central Takeaway

• There is a relationship betwixt the motions of electrons in atoms and molecules and their energies that is described past quantum mechanics.

Conceptual Problems

1. Why does an electron in an orbital with north = one in a hydrogen cantlet have a lower free energy than a free electron (northward = ∞)?

2. What 4 variables are required to fully describe the position of any object in space? In quantum mechanics, one of these variables is not explicitly considered. Which one and why?

3. Chemists generally refer to the foursquare of the wave part rather than to the wave role itself. Why?

4. Orbital energies of species with only one electron are divers past only ane quantum number. Which i? In such a species, is the free energy of an orbital with due north = 2 greater than, less than, or equal to the energy of an orbital with due north = 4? Justify your answer.

5. In each pair of subshells for a hydrogen cantlet, which has the higher energy? Give the principal and the azimuthal quantum number for each pair.

   1. 1due south, iip
   2. iip, 2south
   3. 2s, 3southward
   4. 3d, 4s

6. What is the relationship betwixt the free energy of an orbital and its boilerplate radius? If an electron made a transition from an orbital with an average radius of 846.4 pm to an orbital with an average radius of 476.1 pm, would an emission spectrum or an assimilation spectrum exist produced? Why?

7. In making a transition from an orbital with a principal breakthrough number of four to an orbital with a main quantum number of 7, does the electron of a hydrogen atom emit or blot a photon of energy? What would be the energy of the photon? To what region of the electromagnetic spectrum does this energy correspond?

8. What breakthrough number defines each of the following?

   1. the overall shape of an orbital
   2. the orientation of an electron with respect to a magnetic field
   3. the orientation of an orbital in space
   4. the boilerplate energy and distance of an electron from the nucleus

9. In an attempt to explicate the properties of the elements, Niels Bohr initially proposed electronic structures for several elements with orbits belongings a sure number of electrons, some of which are in the following table:

   Element	Number of Electrons	Electrons in orbits with due north =
   		4	3	2	1
   H	ane				1
   He	2				ii
   Ne	x			8	two
   Ar	18		8	8	2
   Li	3			1	2
   Na	11		ane	eight	2
   K	19	one	8	8	2
   Be	4			2	two

   1. Draw the electron configuration of each cantlet based only on the data given in the table. What are the differences between Bohr'southward initially proposed structures and those accepted today?
   2. Using Bohr'southward model, what are the implications for the reactivity of each element?
   3. Give the actual electron configuration of each element in the table.

10. What happens to the free energy of a given orbital as the nuclear accuse Z of a species increases? In a multielectron atom and for a given nuclear accuse, the Z _eff experienced by an electron depends on its value of l. Why?

11. The electron density of a particular atom is divided into ii general regions. Name these two regions and depict what each represents.

12. As the principal quantum number increases, the energy departure betwixt successive energy levels decreases. Why? What would happen to the electron configurations of the transition metals if this decrease did non occur?

13. Describe the relationship between electron shielding and Z _eff on the outermost electrons of an atom. Predict how chemical reactivity is affected by a decreased effective nuclear accuse.

14. If a given atom or ion has a single electron in each of the following subshells, which electron is easier to remove?

    1. twos, 3s
    2. 3p, ivd
    3. 2p, anesouthward
    4. threed, 4due south

Numerical Issues

1. How many subshells are possible for north = iii? What are they?

2. How many subshells are possible for northward = 5? What are they?

3. What value of 50 corresponds to a d subshell? How many orbitals are in this subshell?

4. What value of l corresponds to an f subshell? How many orbitals are in this subshell?

5. State the number of orbitals and electrons that can occupy each subshell.

   1. twos
   2. threep
   3. 4d
   4. 6f

6. State the number of orbitals and electrons that can occupy each subshell.

   1. onedue south
   2. 4p
   3. 5d
   4. fourf

7. How many orbitals and subshells are institute within the principal crush north = 6? How exercise these orbital energies compare with those for n = 4?

8. How many nodes would yous wait a fourp orbital to have? A vs orbital?

9. A p orbital is found to have ane node in improver to the nodal plane that bisects the lobes. What would you predict to be the value of n? If an southward orbital has 2 nodes, what is the value of n?

Answers

1. Three subshells, with l = 0 (s), l = 1 (p), and fifty = ii (d).

3. A d subshell has l = two and contains 5 orbitals.

5. 1. ii electrons; ane orbital
   2. 6 electrons; three orbitals
   3. 10 electrons; 5 orbitals
   4. 14 electrons; 7 orbitals

7. A chief vanquish with n = 6 contains six subshells, with l = 0, 1, ii, iii, 4, and five, respectively. These subshells contain ane, 3, five, 7, 9, and xi orbitals, respectively, for a total of 36 orbitals. The energies of the orbitals with n = 6 are higher than those of the corresponding orbitals with the aforementioned value of l for north = 4.

Source: https://chem.libretexts.org/Courses/Howard_University/General_Chemistry:_An_Atoms_First_Approach/Unit_1:__Atomic_Structure/Chapter_2:_Atomic_Structure/Chapter_2.5:_Atomic_Orbitals_and_Their_Energies

Posted by: joneswittere.blogspot.com

Share this post